Maximum Depth of N-ary Tree — Day 65(Python)

Photo by Justin Campbell on Unsplash

Today, I thought of solving an N-ary Tree question. Since I have never solved an N-ary Tree question, I thought of starting with something which was tagged easy on leetcode. Let us look into the question without wasting much time.

559. Maximum Depth of N-ary Tree

Given an n-ary tree, find its maximum depth.

The maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value (See examples).

Example 1:

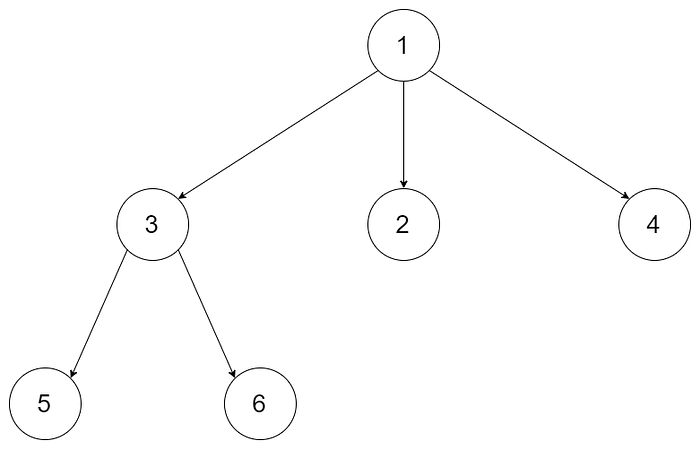
Input: root = [1,null,3,2,4,null,5,6]
Output: 3

Example 2:

Input: root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
Output: 5

Constraints:

• The depth of the n-ary tree is less than or equal to 1000.
• The total number of nodes is between [0, 104].

If this question was asked for a Binary Tree, Breadth-First Search or Depth-First Search would be the algorithm to be used. Can we try using the same logic for an N-ary Tree? What modification do we have to make in order to make the algorithm work?

We will be using the Breadth-First search approach to solve this problem.

We would need a queue that will store the nodes whose children we need to visit next. We will be using another queue that will keep track of all the children of nodes at a particular level. Each time we hit a new level the variable that keeps track of depth will be incremented.

Wait, how do we keep track of children though? We can have a loop that will visit all the children of the required node. Let us look into the code snippet.

class Node:
    def __init__(self, val=None, children=None):
        self.val = val
        self.children = children
class MaxDepthFinder:
    def maxDepth(self, root: 'Node') -> int:
        if root == None:
            return 0
        else:
            depth = 0
            nodes_queue = [root]
            next_nodes_queue = []
            while(nodes_queue):
                node_out = nodes_queue.pop(0)
                for child in node_out.children:
                    next_nodes_queue.append(child)
                if nodes_queue == []:
                    nodes_queue, next_nodes_queue = next_nodes_queue, nodes_queue
                    depth += 1
            return depth

Complexity analysis.

Time Complexity

We are visiting each node once, hence the time complexity is O(N) where N is the number of nodes.

Space Complexity.

We are visiting each node once and storing it in the queue. In the worst case, if all the children are in the same x level, we might have to hold all the nodes in the queue, hence the space complexity is O(N) where N is the number of nodes.